

High-resolution dataset [13MB] and ground-truths
Low-resolution dataset [4MB] and ground-truths
The registration of non-rigidly deforming shapes is a fundamental problem in the area of Graphics and Computational Geometry. One of the applications of shape registration is to facilitate 3D model retrieval; after alignment it becomes easier to compare shapes since the correspondences between their elements is known. Many existing methods have been proposed for computing shape correspondence [van Kaick et al., 2011, Tam et al., 2013, Sahillioğlu, 2019]. These approaches assume surface deformations to be simple (i.e., primarily piece-wise rigid) and contain low degrees of non-isometry. Presently, there are currently few public datasets that challenge these concepts, providing complex real-world deformations. Few benchmarking datasets suitably consider the different types of extreme deformation that an object may undergo in real-life, and typically only consider synthetic or near-isometric deformations.
This motivates our track which provides a new benchmark that consists of real-life shapes that undergo varying types of complex deformation. The findings of this track will be presented at the Workshop on 3D Object Retrieval in Graz, Austria, 4-5 September 2020 and is in collaboration with Eurographics (pending) and Elsevier.
To participate in this track, please register by emailing DykeRM@cardiff.ac.uk
For queries, contact the corresponding organiser at roberto-marco.dyke@inria.fr
For this track we have produced a new dataset from 3D scans of a real-world object, captured by ourselves using a high-precision 3D scanner (Artec3D Space Spider) designed for small objects. Each scan exhibits one or more types of deformation. We classify these objects into four distinct groups by the type of deformation primarily exhibited:
We further increase the challenge of our task by varying the internal properties of the object by filling it with different materials (illustrated below). This causes incremental changes to the deformation ehibited.

Cousous

Risotto rice

Chickpeas
Partial scans
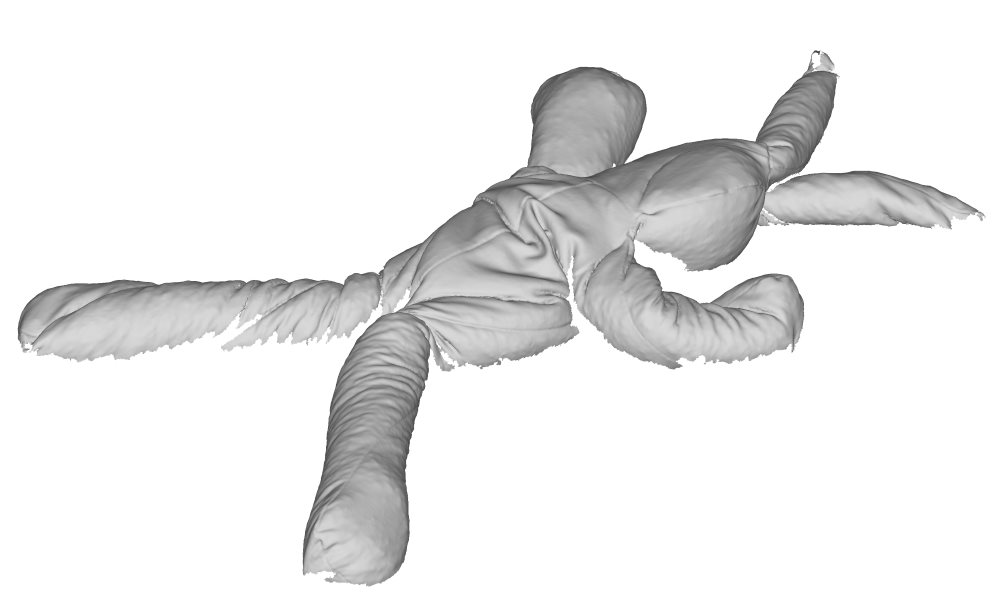
Complex deformations
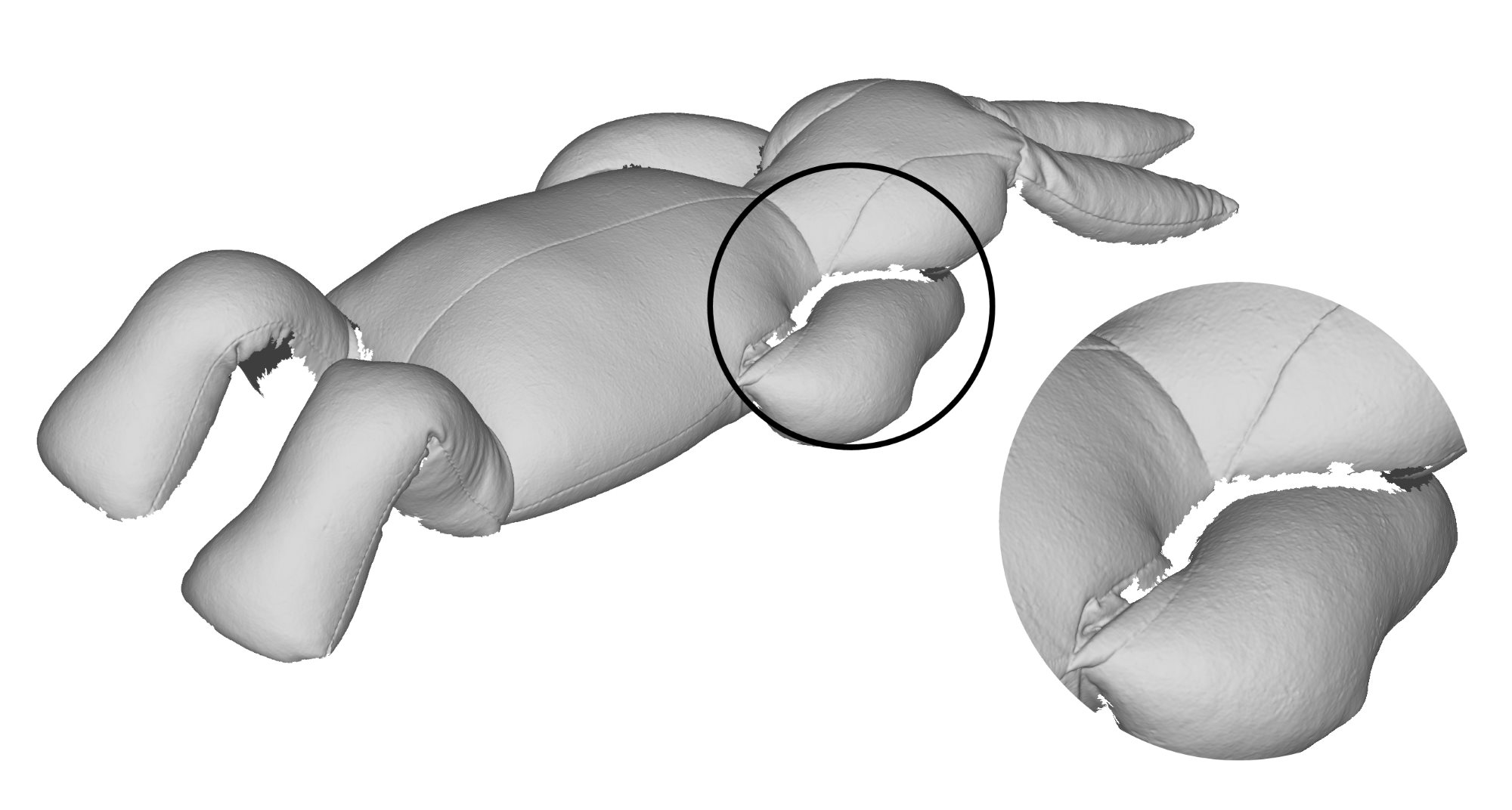
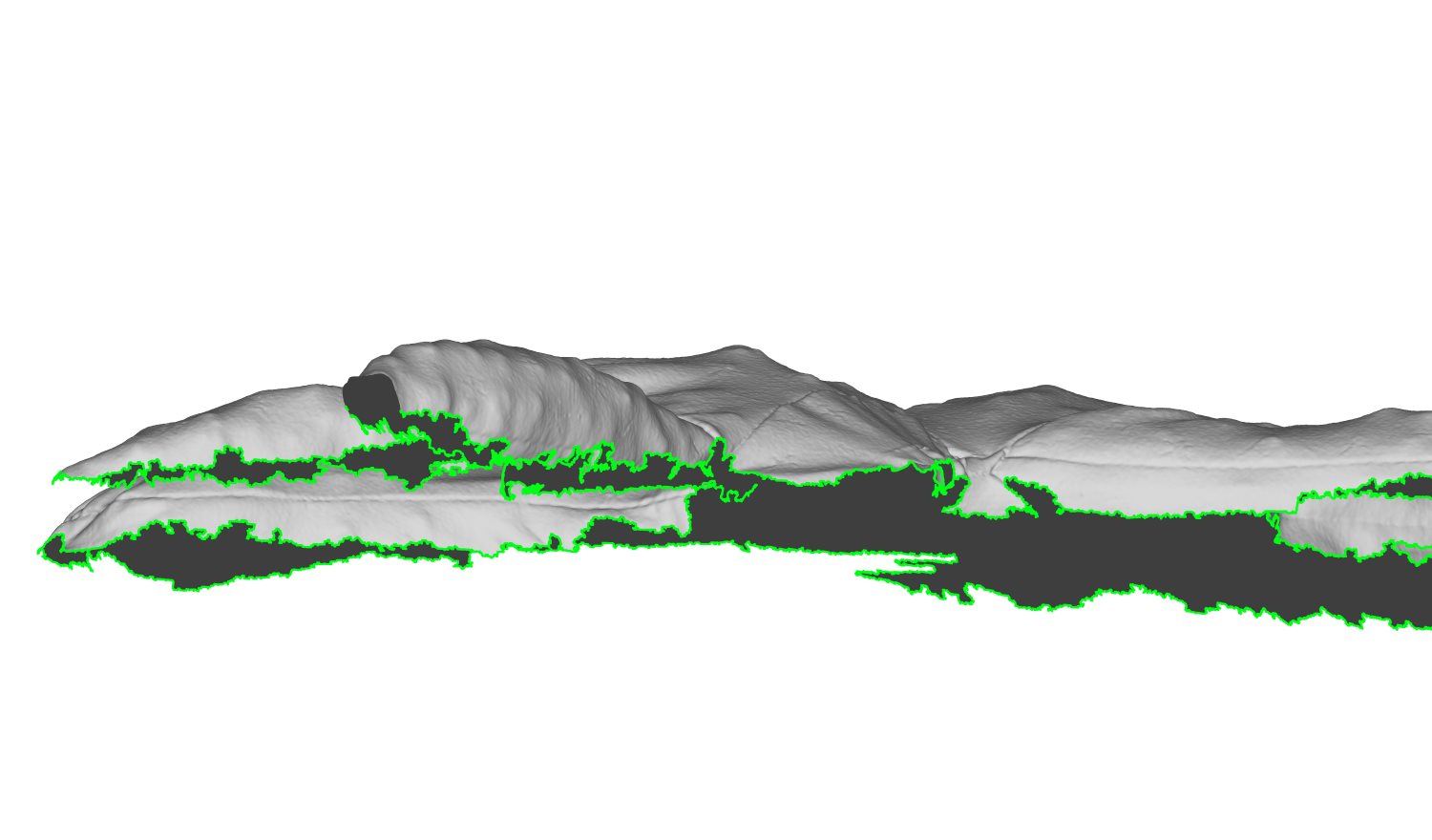
Missing geometry caused by self-occlusion
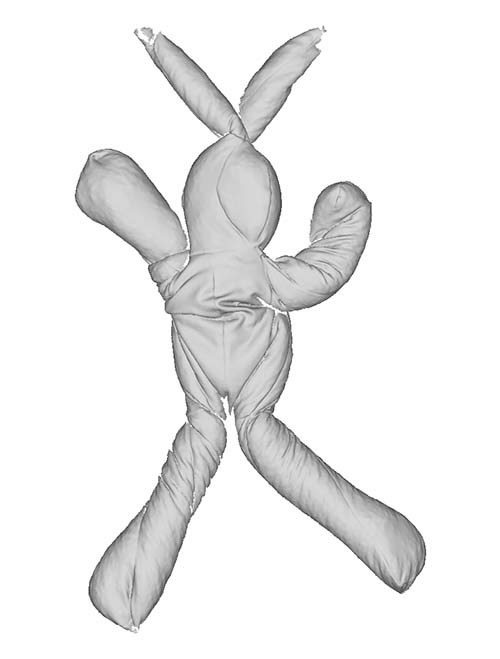
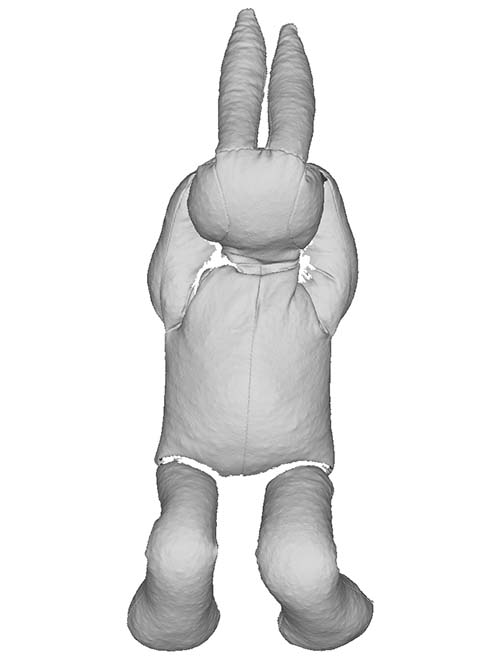
The dataset consists of a stuffed toy rabbit made out of a stretchy jersey material with no type of internal skeleton that could otherwise further restrict its movement. The rabbit is covered with coloured markers, which allow us to acquire accurate ground truths. The rabbit is captured in a set of poses that exhibit the aforementioned deformations. Furthermore, we fill the rabbit with different materials that cause the rabbit to appear and deform in different ways when positioned in the same pose. The rabbit was filled with three different materials that went from coarse to fine grained. We have carefully selected poses and materials that incrementally introduce these deformation challenges so that the limitations (w.r.t. these varying properties) can be clearly identified. Some examples of challenging cases are shown in the figure above.
The dataset contains 11 partial scans and one full scan, for the purposes of the benchmark this dataset is a sufficient size for our evaluation. Each scan represents a unique combination of pose and internal material (illustrated in below). Participants will be required to find correspondences for all scan pairs.
All scans are converted into triangulated and watertight meshes. Meshes are simplified to both 80,000 triangles and 20,000 triangles.
Ground-truth correspondences have been produced between surfaces of different scans of the same object using texture markers. These will not be made available to participants and are reserved for evaluation of participant entries.
Partial scans |
|||
|---|---|---|---|
| Couscous | Risotto rice | Chickpea | |
| Stretch |  |
 |
|
| Indent | 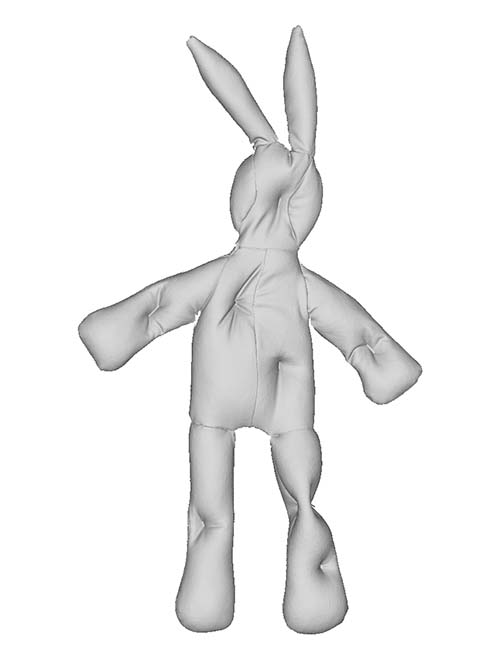 |
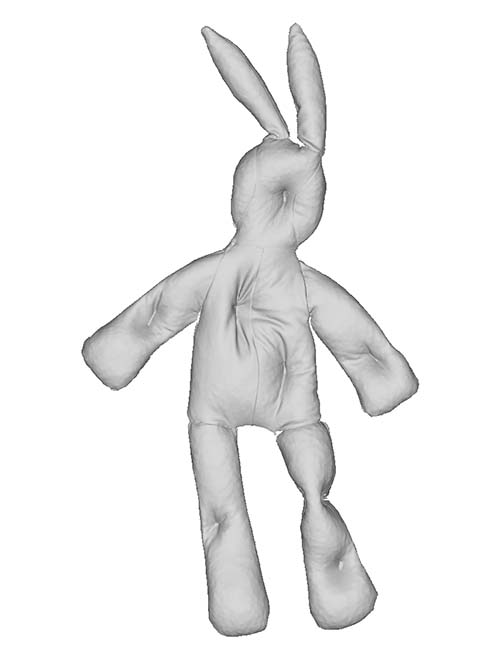 |
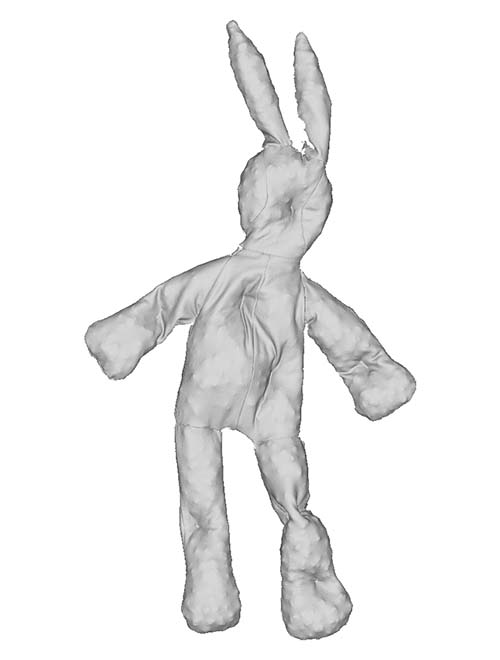 |
| Twist |  |
 |
 |
| Inflate |  |
 |
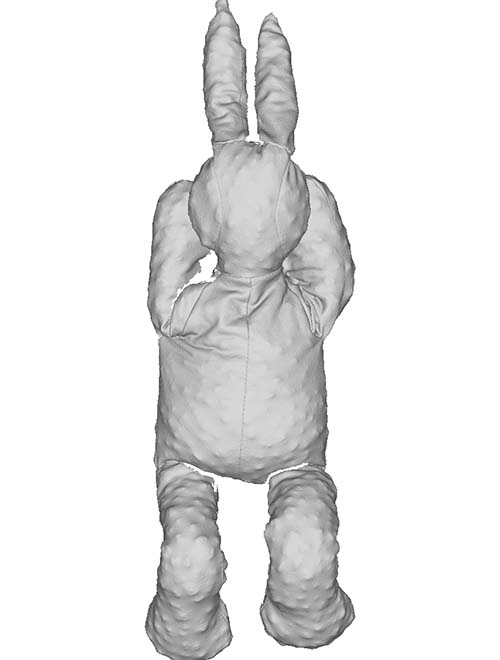 |
Full scan |
|||
| T-pose | 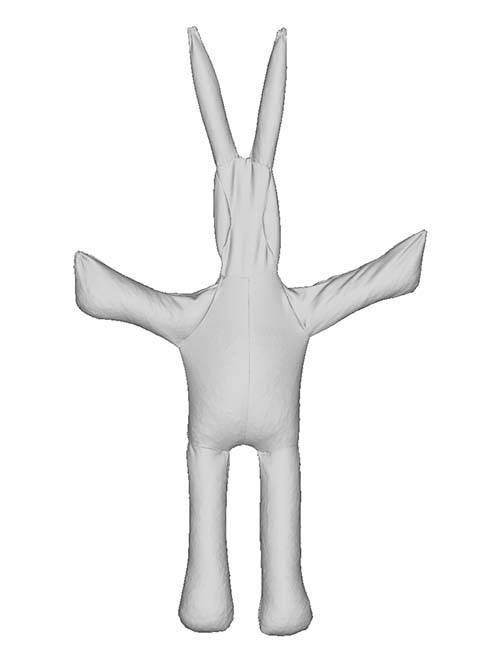 |
||
Participants are provided a copy of the dataset. Participants are to find the correspondence between each partial scan and the one watertight scan. As well as their results, participants will be asked to also submit a description of the method used. Participants should mention any changes made to internal parameters between scans pairs.
The quality of shape correspondence will be evaluated by the organisers automatically using normalised geodesics to measure the distance between the ground-truth and predicted correspondence. Similarly to other shape correspondence benchmarks [Cosmo et al., 2016, Lähner et al., 2016], we will evaluate the correspondence quality of each method using the approach of Kim et al. [2011]. We shall use the following measurements to help evaluate the performance of each method:
Let
be a pair of correspondences between the surface of a partial scan
and the surface of the full scan
, the normalised geodesic error
between the predicted correspondence
and the ground-truth position
on surface
is measured as:
For methods that produce a sparse correspondence, we shall interpolate their result and measure the predicted correspondence against the ground truth.
Participants must match all partial scans to the full scan. A short description of the algorithm/method used must be included with a submission. Either dense or sparse vertex-to-face correspondences for each scan pair may be submitted. Participants should email a zipped file containing their results to DykeRM@cardiff.ac.uk. If participants are unable send their results directly via email, e.g., because the file is too large, they may share their results via other platforms.
Like Cosmo et al. [2016], for each scan pair, participants shall give the correspondence for each vertex on
a partial scan
to a barycentric co-ordinate on the surface of the full scan
in a four column file, as follows:
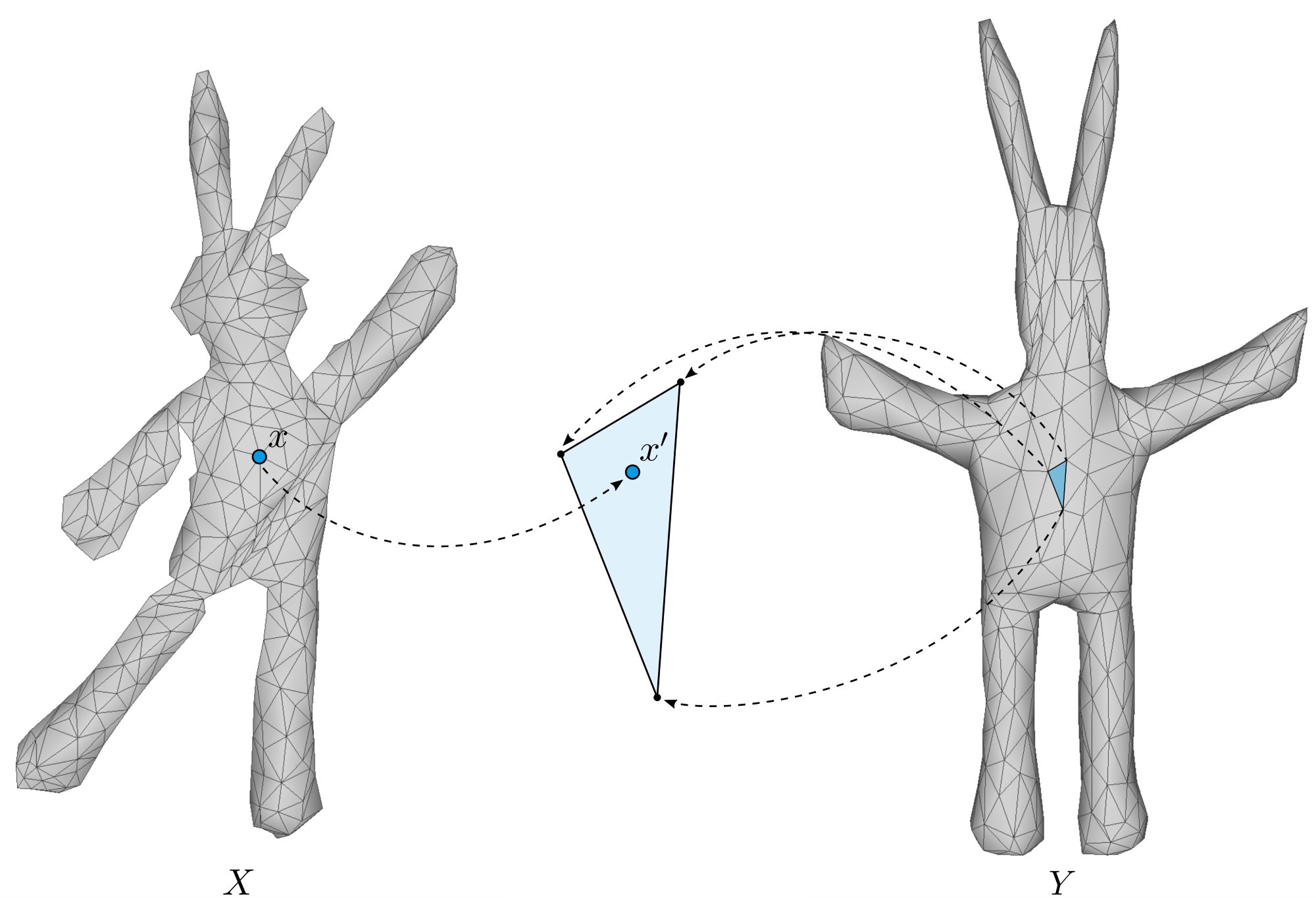
The diagram below illustrates how the predicted correspondence
is represented on surface
as a barycentric co-ordinate on a face of
.
G. Andrews, S. Endean, R. Dyke, Y. Lai, G. Ffrancon, and G. K. L. Tam. HDFD — A high deformation facial dynamics benchmark for evaluation of non-rigid surface registration and classification. CoRR, abs/1807.03354, 2018. URL http://arxiv.org/abs/1807.03354.
F. Bogo, J. Romero, M. Loper, and M. J. Black. FAUST: Dataset and evaluation for 3D mesh registration. In Proceedings IEEE Conf. on Computer Vision and Pattern Recognition. IEEE, 2014. doi: 10.1109/CVPR.2014.491.
L. Cosmo, E. Rodolà, M. M. Bronstein, A. Torsello, D. Cremers, and Y. Sahillioğlu. Partial matching of deformable shapes. In Proceedings of the Eurographics 2016 Workshop on 3D Object Retrieval, 3DOR'16, Goslar, Germany, 2016. ISBN 978-3-03868-004-8. doi: 10.2312/3dor.20161089.
V. G. Kim, Y. Lipman, and T. Funkhouser. Blended intrinsic maps. In ACM SIGGRAPH 2011 Papers, SIGGRAPH'11, pages 79:1-79:12, New York, NY, USA, 2011. ACM. ISBN 978-1-4503-0943-1. doi: 10.1145/1964921.1964974.
Z. Lähner, E. Rodolà, M. M. Bronstein, D. Cremers, O. Burghard, L. Cosmo, A. Dieckmann, R. Klein, and Y. Sahillioğlu. Matching of Deformable Shapes with Topological Noise. In Eurographics Workshop on 3D Object Retrieval, 2016. ISBN 978-3-03868-004-8. doi: 10.2312/3dor.20161088.
Y. Sahillioğlu. Recent advances in shape correspondence. The Visual Computer, September 2019. doi:10.1007/s00371-019-01760-0.
G. K. L. Tam, Z. Cheng, Y. Lai, F. C. Langbein, Y. Liu, D. Marshall, R. R. Martin, X. Sun, and P. L. Rosin. Registration of 3d point clouds and meshes: A survey from rigid to nonrigid. IEEE Transactions on Visualization and Computer Graphics, 19(7):1199-1217, July 2013. ISSN 1077-2626. doi: 10.1109/TVCG.2012.310.
O. van Kaick, H. Zhang, G. Hamarneh, and D. Cohen-Or. A survey on shape correspondence. Computer Graphics Forum, 30(6):1681-1707, 2011. doi: 10.1111/j.1467-8659.2011.01884.x.
@inproceedings {Dyke:2020:track.a,
booktitle = {Eurographics Workshop on 3D Object Retrieval},
editor = {Schreck, Tobias and Theoharis, Theoharis and Pratikakis, Ioannis and Spagnuolo, Michela and Veltkamp, Remco C.},
title = {{SHREC 2020 Track}: Non-rigid Shape Correspondence of Physically-Based Deformations},
author = {Dyke, Roberto M. and Zhou, Feng and Lai, Yu-Kun and Rosin, Paul L. and Guo, Daoliang and Li, Kun and Marin, Riccardo and Yang, Jingyu},
year = {2020},
publisher = {The Eurographics Association},
ISSN = {1997-0471},
ISBN = {978-3-03868-126-7},
DOI = {10.2312/3dor.20201161}
}