Shape Correspondence with Non-Isometric Deformations

A dataset of highly non-isometric non-rigid quadruped shapes with consensus-based ground-truth correspondences.

The paper is available online: Download paper [2MB]

Download Dataset

High-resolution dataset [10MB] and ground-truths
Low-resolution dataset [3MB] and ground-truths

Download Evaluation Code

The coverage measure — a novel measure of the distribution and sparsity of correspondences.

Introduction

The registration of non-rigidly deforming shapes is a fundamental problem in the area of Graphics and Computational Geometry. One of the applications of shape registration is to facilitate 3D model retrieval; after alignment it becomes easier to compare shapes since the correspondences between their elements is known. Many existing methods have been proposed for computing shape correspondence [van Kaick et al., 2011, Tam et al., 2013, Sahillioğlu, 2019]. These approaches assume surface deformations to be simple (i.e., primarily piece-wise rigid) and contain low degrees of non-isometry.

Presently, there are few public datasets that provide challenging non-isometric deformations, this motivates our track. We focus on exploiting existing data from a variety of sources to construct a new high-quality dataset that contains large scale non-rigid deformations, which have high degrees of non-isometry. The findings of this track will be presented at the Workshop on 3D Object Retrieval in Graz, Austria, 4-5 September 2020 and is in collaboration with Eurographics (pending) and Elsevier.

~~To participate in this track, please register by emailing DykeRM@cardiff.ac.uk~~

For queries, contact the corresponding organiser at roberto-marco.dyke@inria.fr

Important dates

March 16, 2020: Participant submit results for this track, participants must also include a short description of their method, submitted to ~~DykeRM@cardiff.ac.uk~~.
April 03, 2020: This track is finished, and results are included in a track report are submitted for review.

Organisers

Roberto M. Dyke — Cardiff University, UK.
Yu-Kun Lai — Cardiff University, UK.
Paul L. Rosin — Cardiff University, UK.

Dataset

For this track we have identified a set of synthetic models and real-world scans of 3D shapes and produced a set of ground truth correspondences. Shapes have been cleaned up to remove major errors such as self-intersecting faces and handles which erroneously cause a high genus. Correspondences have been acquired by asking experts in geometry processing to label the shapes manually. For each correspondence, multiple experts propose a point on the surface and we found a consensus by selecting the medoid of these points. Because the dataset primarily consists of real-world scans acquired using different techniques, it also represents challenges that are present in most acquisition methods (e.g., geometric inconsistencies and topological changes caused by self-contact). The real-scans also contain natural noise, varying triangulation and self-occluded geometry. Some examples of challenging cases are shown below.

Illustrations of some of the challenges in our dataset.

Partial scans (green indicates the boundary)

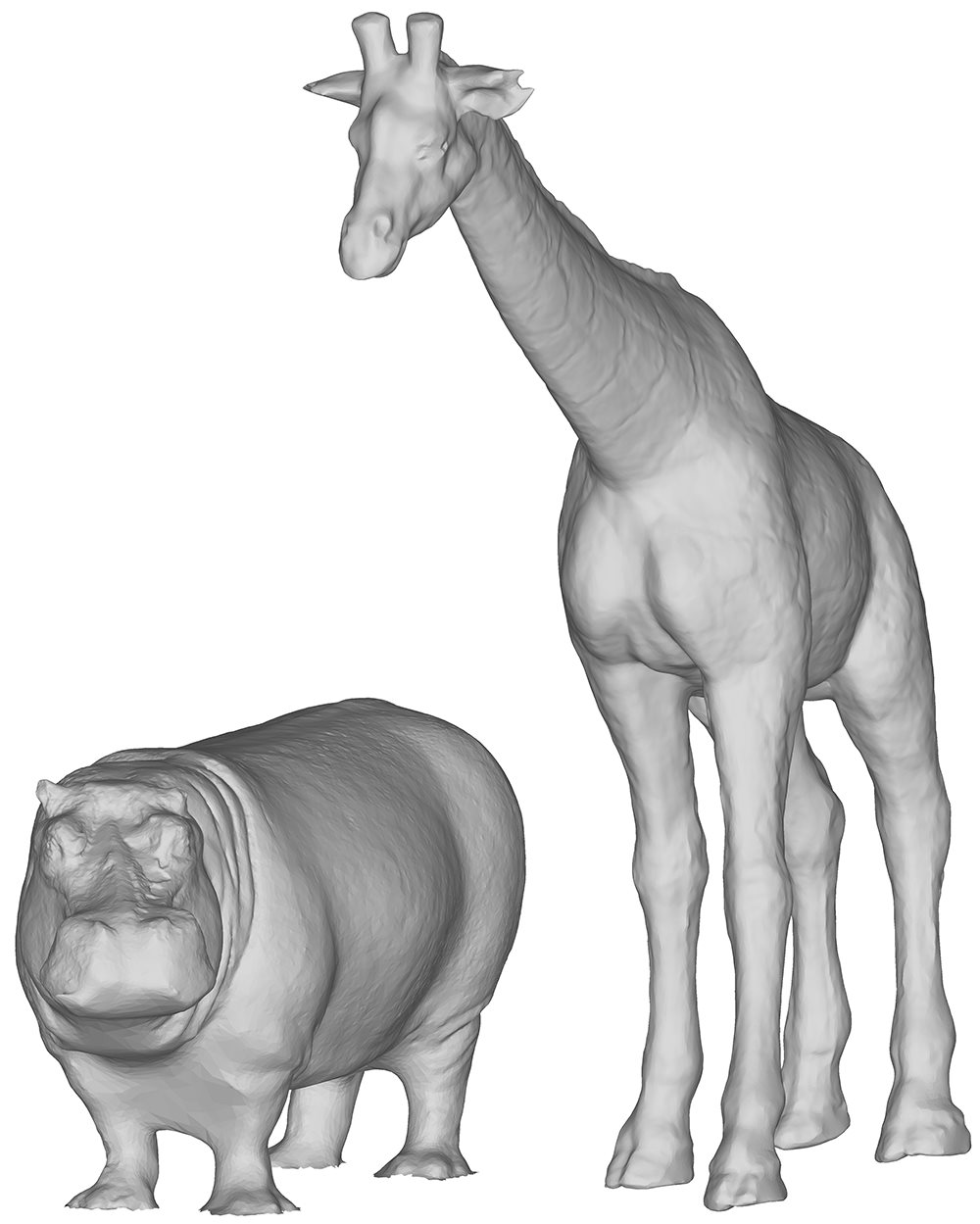
Significant non-isometric deformations

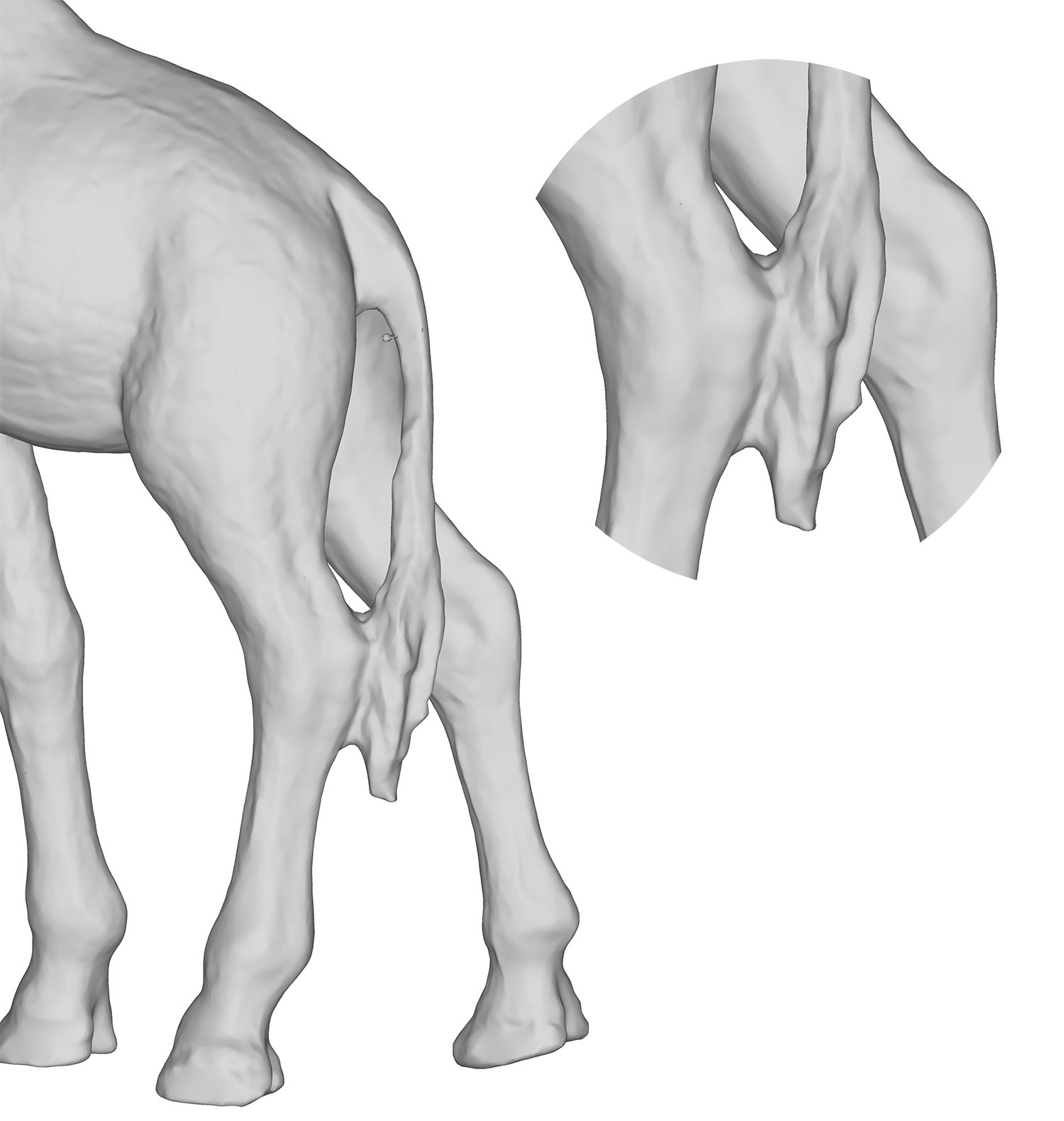
Topological inconsistencies from scanning

The dataset contains 14 models that have been acquired using a variety of techniques (see table below). Because the dataset is limiited to tetrapods only, we are able to establish sensible correspondences between features the shapes share in common (e.g. legs, neck, tail, etc.). There are $P(14,2)=210$ permutations of shape pairs. For our benchmarking experiment we shall ask participants to complete a subset of these pairs comprising of matching pairs of full-to-full and partial-to-full models. The ground-truths for this dataset are acquired using the originally sourced mesh.

For the benchmark, where models have an exceedingly high triangle count, the mesh is simplified to 100,000 triangles. Participants may also submit results using a low-resolution version of the meshes with 20,000 triangles that will also be made available.

Ground-truth correspondences will not be made available to participants and are reserved for evaluation of contest entries. These will be publicly released subsequent to the completion of this track.

Source	Acquisition method	Provisional name	Author
Sketchfab.com	Metashape by Agisoft	bison	misterdevious
	NextEngine 3D Scanner	leopard	Moshe Caine
	EinScan-S 3D Scanner	giraffe_a	SHINING 3D
	COLMAP with 20 Canon G16 cameras	rhino	DigitalLife3D & Perth zoo
	Sprout Pro by HP	pig	Lindy
	Metashape by Agisoft	elephant_a	Spogna
	Metashape by Agisoft	dog	Spogna
	Recap360 by Autodesk with an iPhone	hippo	Alban Denoyel
AIM@SHAPE-VISIONAIR	Synthetic	cow	Anita Parodi
	Unknown	giraffe_b	Anita Parodi
	Polhemus FastScan laser scanner	bear	Ira Kemelmacher
	Polhemus FastScan laser scanner	camel_b	Ira Kemelmacher
	Synthetic	camel_a	Inria & ISTI
	Konica-Minolta Vivid 910	elephant_b	Inria & ISTI

Tasks

Participants are to find the correspondence between each shape pair specified. Along with their results, participants will be asked to submit a description of the method used. Participants should mention any changes made to internal parameters between test-sets. We expect this task to require little time to complete, thus the turn-around time for this track will be short.

Evaluation

The quality of shape correspondence will be evaluated by the organisers systematically using normalised geodesics to measure the distance between the ground-truth and predicted correspondence. Similarly to other shape correspondence benchmarks [Cosmo et al., 2016, Lähner et al., 2016], we will evaluate the correspondence quality of each method using the approach of Kim et al. [2011]. We shall use the following measurement to help evaluate the performance of each method:

For methods that complete all scan pairs, an overall error measurement will be based on the number of correspondences within a normalised geodesic threshold, this will be used to plot cumulative error curves.

Let $(x_i,x_i') \in X \times Y$ be a pair of correspondences between the surface of a partial scan $X$ and the surface of the full scan $Y$ , the normalised geodesic error $\epsilon_i$ between the predicted correspondence $x_i'$ and the ground-truth position $y_i^*$ on surface $Y$ is measured as:

$\epsilon(x_i) = \frac{d_Y(x_i',y_i^*)}{ \mathrm{area}(Y)^{1/2} }$

For methods that produce a sparse correspondence, we shall interpolate their result and measure the predicted correspondence against the ground truth.

Submission

The dataset has been divided into several discrete sets. Participants are expected to complete at least one of the sets. A short description of the algorithm/method used must be included with a submission. Either dense or sparse vertex-to-face correspondences for each scan pair may be submitted. Participants should email a zipped file containing their results to ~~DykeRM@cardiff.ac.uk~~. If participants are unable send their results directly via email, e.g., because the file is too large, they may share their results via other platforms.

Registration Format

Like Cosmo et al. [2016], for each scan pair, participants shall give the correspondence for each vertex on a partial scan $X$ to a barycentric co-ordinate on the surface of the full scan $Y$ in a four column file, as follows:

Each row represents the vertex on the target scan (i.e., the ith row = the ith vertex).
The first column contains a one-based index of the triangle on the source shape that the matched point is predicted to lie on. Points that participants fail to match should use the index value -1.
The second, third and fourth columns represent the barycentric weights of the matched point.

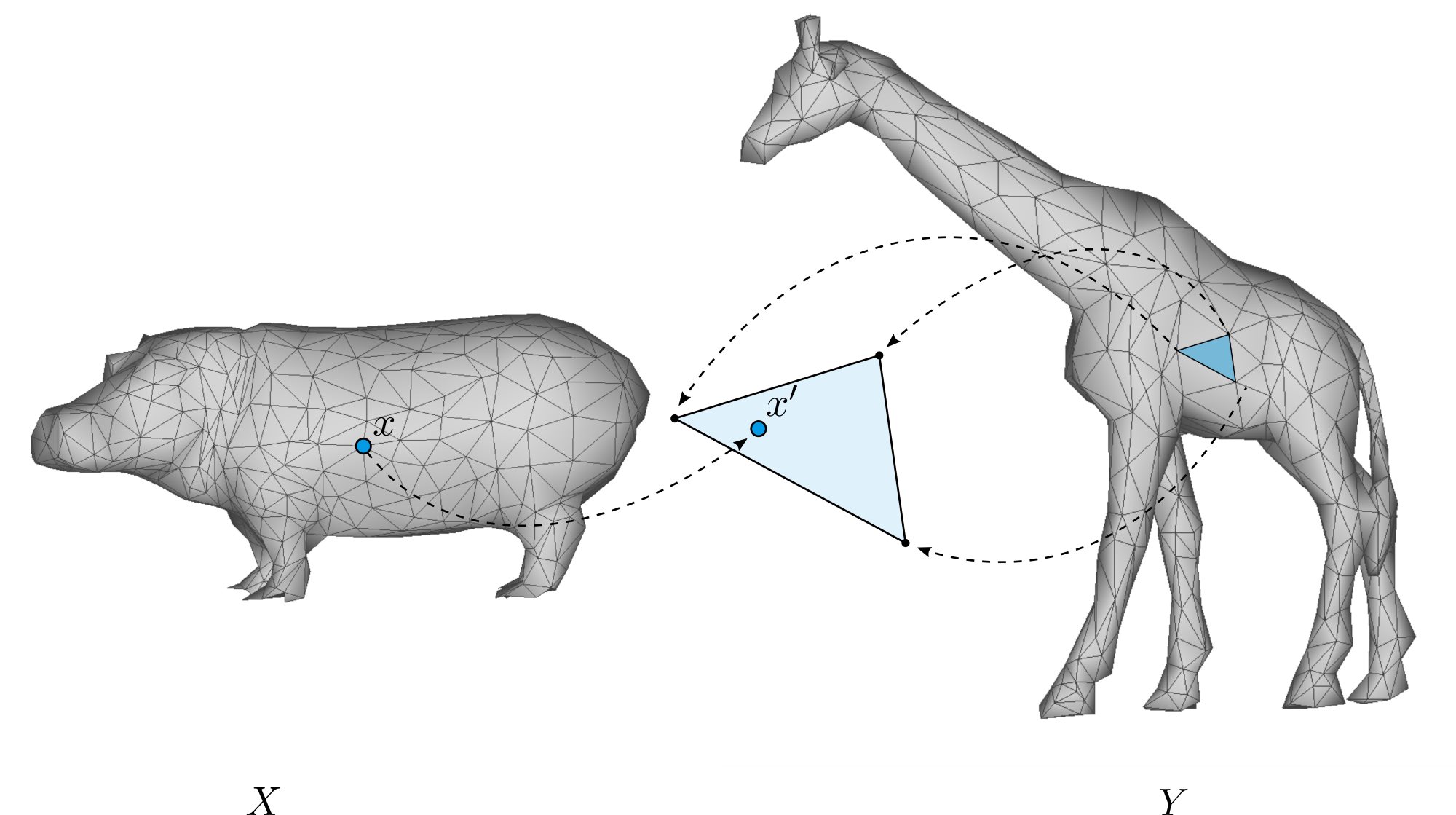
The diagram below illustrates how the predicted correspondence $(x_i,x_i')$ is represented on surface $Y$ as a barycentric co-ordinate on a face of $Y$ .

References

G. Andrews, S. Endean, R. Dyke, Y. Lai, G. Ffrancon, and G. K. L. Tam. HDFD — A high deformation facial dynamics benchmark for evaluation of non-rigid surface registration and classification. CoRR, abs/1807.03354, 2018. URL http://arxiv.org/abs/1807.03354.

F. Bogo, J. Romero, M. Loper, and M. J. Black. FAUST: Dataset and evaluation for 3D mesh registration. In Proceedings IEEE Conf. on Computer Vision and Pattern Recognition. IEEE, 2014. doi: 10.1109/CVPR.2014.491.

L. Cosmo, E. Rodolà, M. M. Bronstein, A. Torsello, D. Cremers, and Y. Sahillioğlu. Partial matching of deformable shapes. In Proceedings of the Eurographics 2016 Workshop on 3D Object Retrieval, 3DOR'16, Goslar, Germany, 2016. ISBN 978-3-03868-004-8. doi: 10.2312/3dor.20161089.

V. G. Kim, Y. Lipman, and T. Funkhouser. Blended intrinsic maps. In ACM SIGGRAPH 2011 Papers, SIGGRAPH'11, pages 79:1-79:12, New York, NY, USA, 2011. ACM. ISBN 978-1-4503-0943-1. doi: 10.1145/1964921.1964974.

Z. Lähner, E. Rodolà, M. M. Bronstein, D. Cremers, O. Burghard, L. Cosmo, A. Dieckmann, R. Klein, and Y. Sahillioğlu. Matching of Deformable Shapes with Topological Noise. In Eurographics Workshop on 3D Object Retrieval, 2016. ISBN 978-3-03868-004-8. doi: 10.2312/3dor.20161088.

Y. Sahillioğlu. Recent advances in shape correspondence. The Visual Computer, September 2019. doi:10.1007/s00371-019-01760-0.

G. K. L. Tam, Z. Cheng, Y. Lai, F. C. Langbein, Y. Liu, D. Marshall, R. R. Martin, X. Sun, and P. L. Rosin. Registration of 3d point clouds and meshes: A survey from rigid to nonrigid. IEEE Transactions on Visualization and Computer Graphics, 19(7):1199-1217, July 2013. ISSN 1077-2626. doi: 10.1109/TVCG.2012.310.

O. van Kaick, H. Zhang, G. Hamarneh, and D. Cohen-Or. A survey on shape correspondence. Computer Graphics Forum, 30(6):1681-1707, 2011. doi: 10.1111/j.1467-8659.2011.01884.x.

Cite paper

@article{Dyke:2020:track.b,
 journal = {Computers \& Graphics},
 title = {{SHREC'20}: Shape correspondence with non-isometric deformations},
 author = {Roberto M. Dyke and Yu-Kun Lai and Paul L. Rosin and Stefano Zappal{\`a} and Seana Dykes and Daoliang Guo and Kun Li and Riccardo Marin and Simone Melzi and Jingyu Yang},
 volume = {92},
 pages = {28-43},
 year = {2020},
 ISSN = {0097-8493},
 DOI = {10.1016/j.cag.2020.08.008},
 URL = {http://www.sciencedirect.com/science/article/pii/S0097849320301266},
}